最近看到一篇GPS工作原理的文章: 中文翻译版:https://pages.longtian.info/gps/ 英文原文:https://ciechanow.ski/gps/. 发现质量挺高的. 页面内容有很多交互式类似h5的页面.

(为了防止原页面丢失, 这里保存了下来: gps工作原理.rar)

有空的时候,可以研究一下.

基本原理

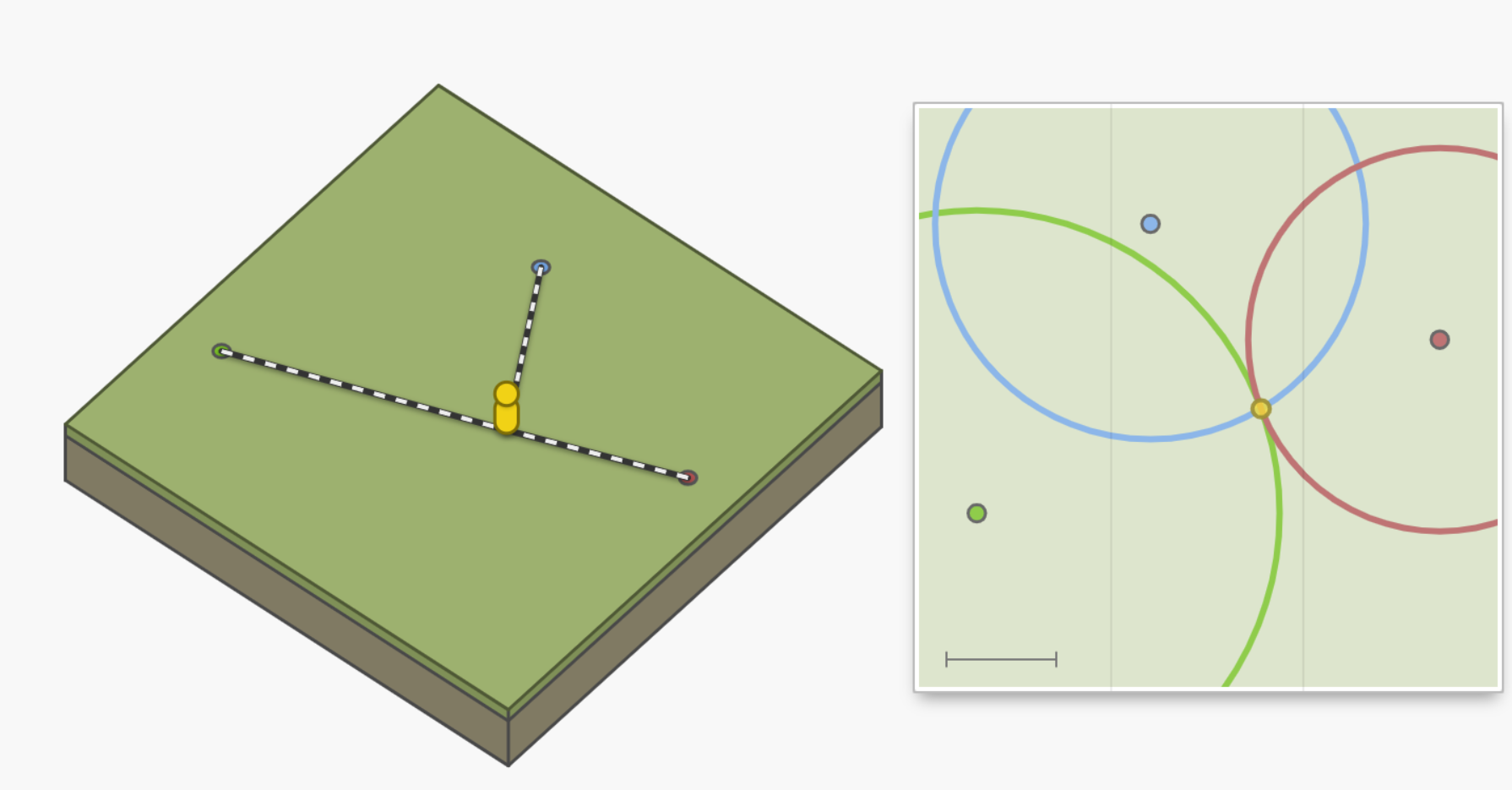
  • 通过到3点的距离,确定位置(自己的位置在以3个点为圆心,各个距离为半径的圆的交点) image.png
  • 用时间计算距离(选定一个恒定速度的传播介质,传播信号,利用信号发出和接受到的时间差,计算出距离)
    • 信号从哪里发出?
      • 方案1(主动系统): 从自己发出,监测点接收. 不可行
        • 在这样的系统里地标会主动的响应使用者获得信息的请求。 一旦使用者增多，系统的复杂性就会大幅地增加。 即使我们想出巧妙的方法来让地标甄别输入信号并给出不同的响应，也无法保证不会有部分用户使整个系统过载.
      • 方案2(被动系统): 监测点(地标)发出信号,使用者接收信号. 实际的方案
        • 解决了系统过载的问题. 监测点总是在固定的时间点(如每分钟的0秒)发出信号.
        • 遇到的问题
          • 用户时钟和系统时钟可能不能总是保持一致. 从而造成计算出的时间有误差,使得最终无法准确测量距离.
        • 解决用户时钟和系统时钟不同步的问题
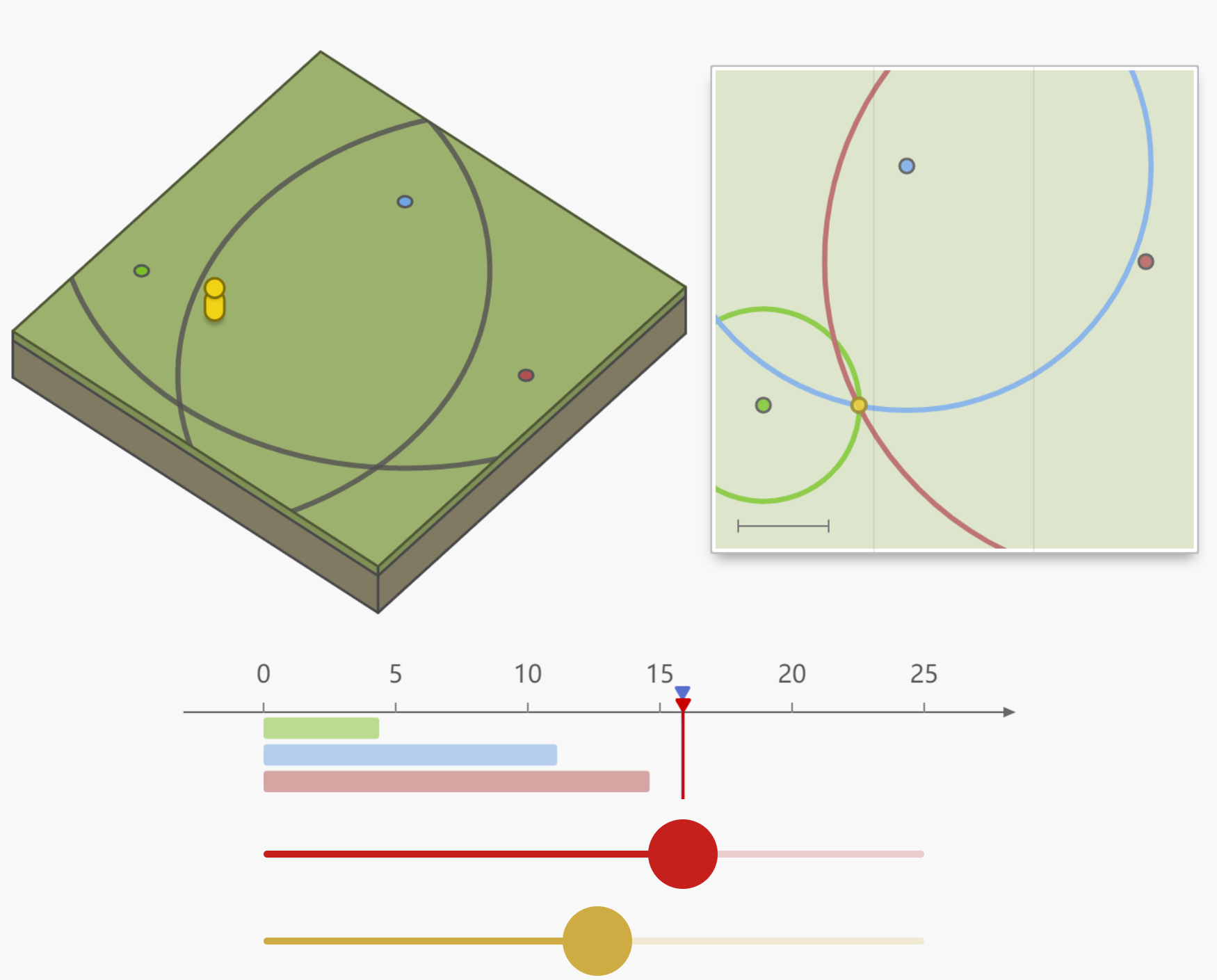
          • 保证监测点的系统时钟是一致的. 因为所有的地标的有相同 系统时间 ， 所以 我们的时钟 和每个地标的 偏差 是一模一样的. 因为这个 偏差 是相同的， 所以三个计算得出的距离都是要么 一起 偏短，要么 一起 偏长。 当我们收到所有 三个信号后， 我们可以试着猜这个 偏差 的具体是多少， 只有 唯一的一个偏差值 能够让三个圈在同一个点交汇，这个点正是我们在地图上的位置。 image.png
          • 引入第三个位置已知的发射器,我们不仅准确地计算出了位置，而且连 用户时钟 时钟的 偏差 也得到了。 这就让我们可以将 用户时钟 和 定位系统的时钟 同步 - 这样我们就获得了一个准确时间的可靠来源.
  • 从平面升级到3D空间
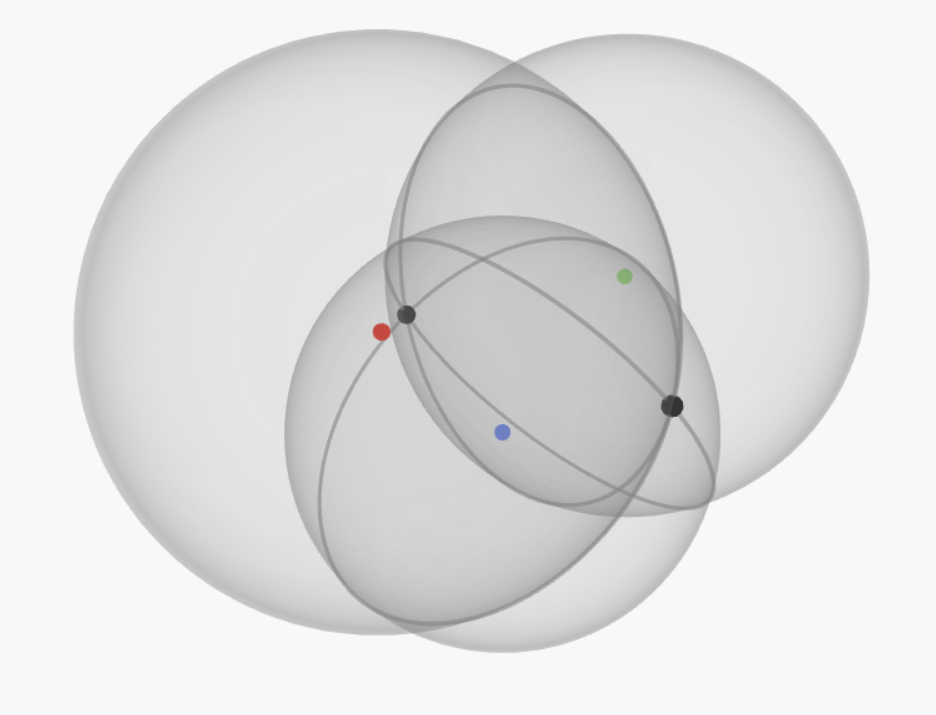
    • 平面上的圆圈需要升级为空间中的球面,3个球面可以相交于2个点: image.png
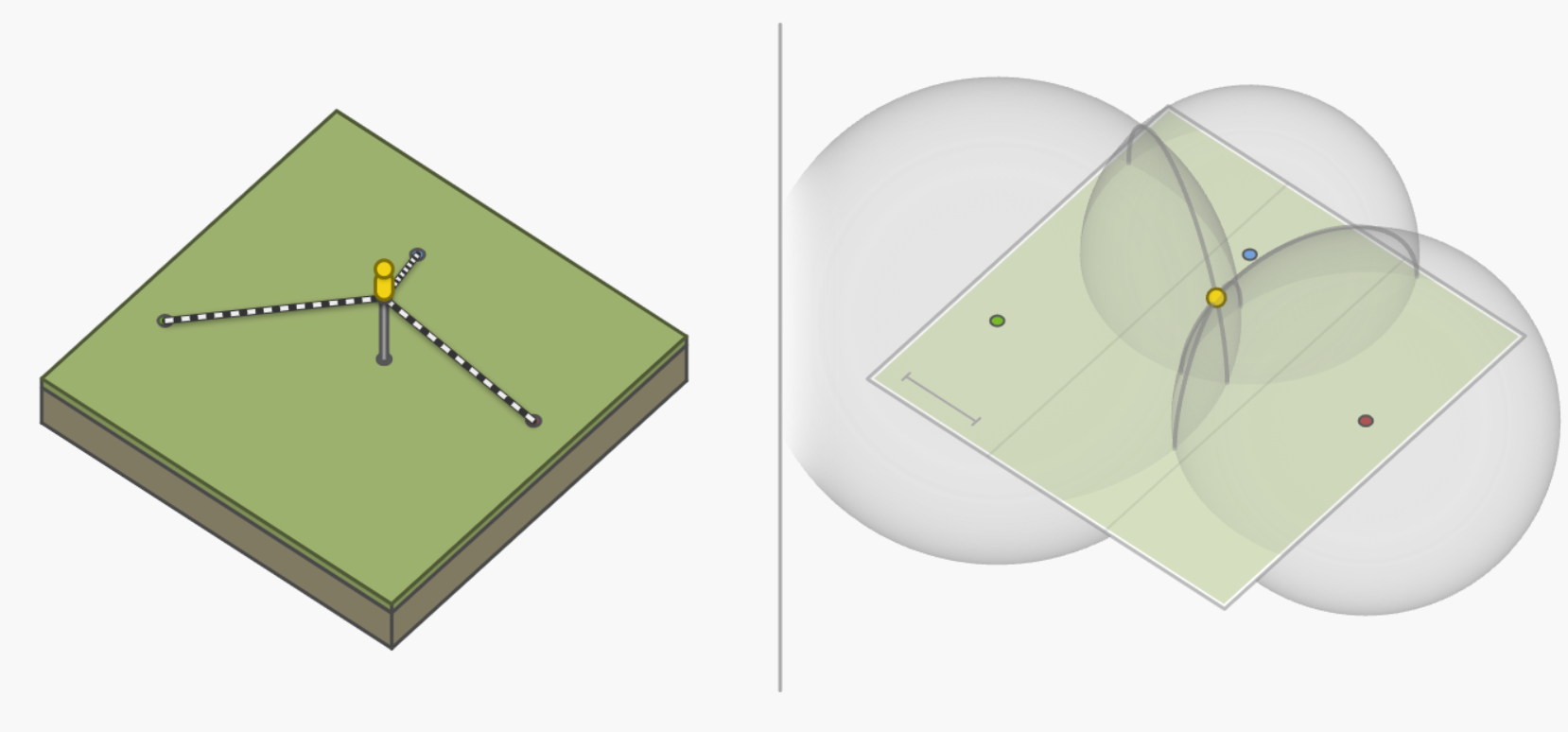
    • 但如果考虑到实际的使用场景, 这2个点一个在地面之上,一个在地面之下, 所以3个发射器,就可以唯一无歧义的确定自己在空间中的位置了(位置和高度). image.png
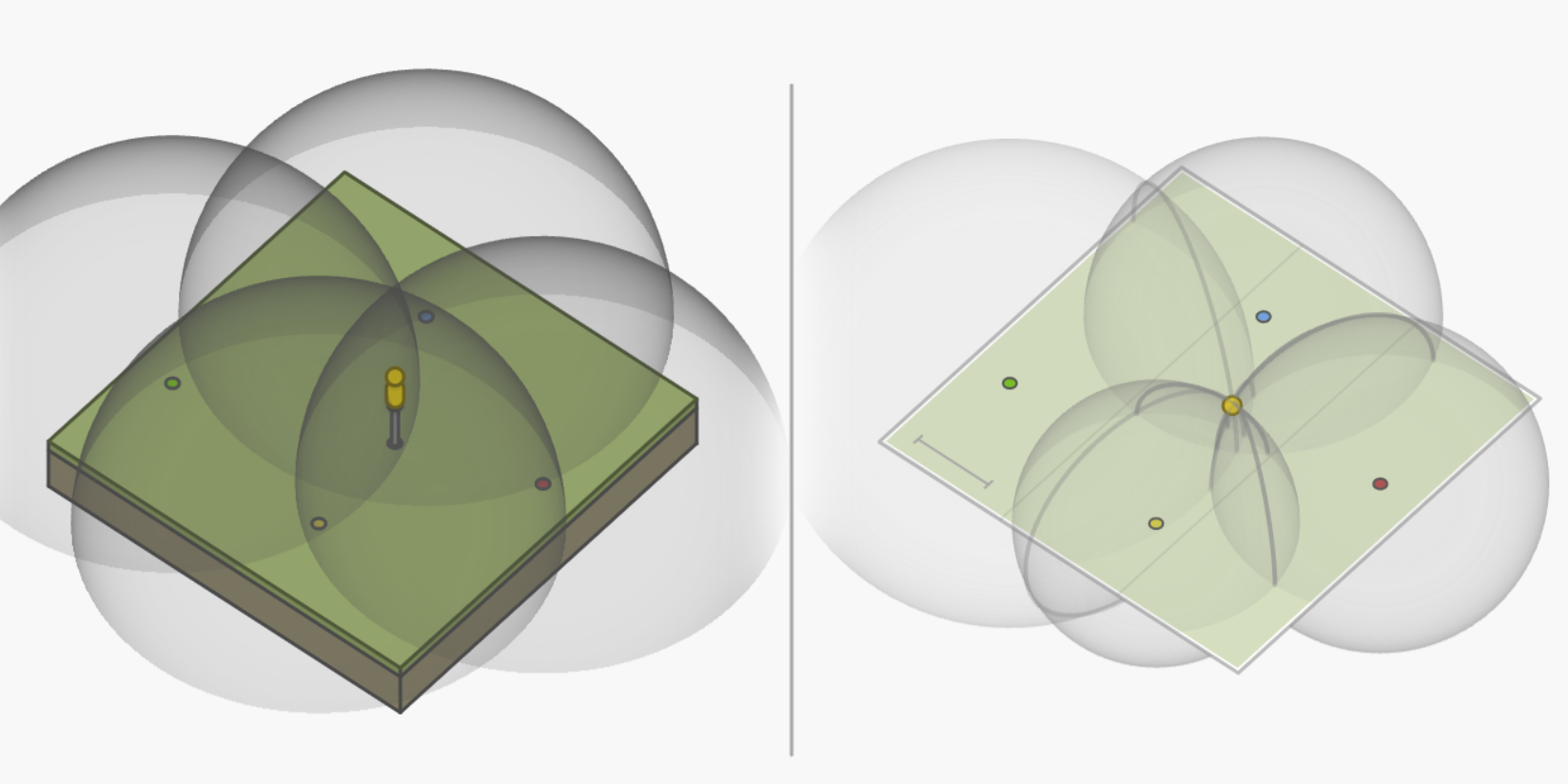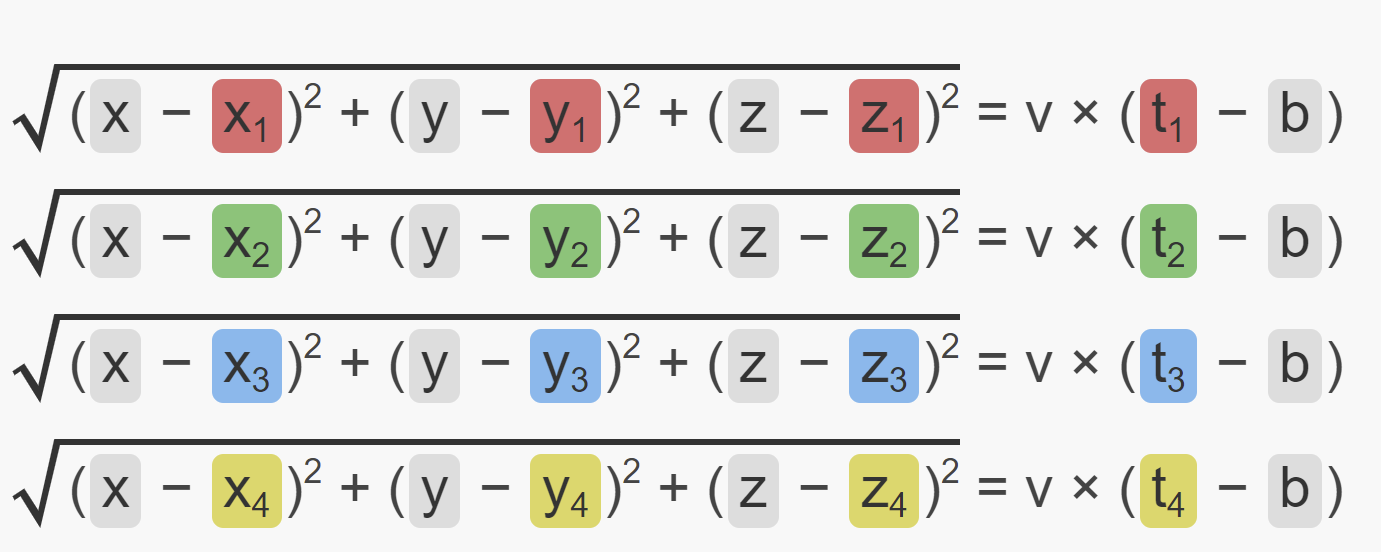    • 类似于平面的场景,当用户没有和系统完美同步的时钟时, 只用3个发射器, 会找到多个不同的偏差, 让三球相交于一点. 从而无法确定偏差. 这时引入第四个发射点, 可以解决这个问题. image.png **需要至少四个发射装置来计算伪距的方法 正是 GPS 用的来计算接收器位置和时钟偏差的方法. **背后的数学原理: 我们要处理到四个发射器距离，归结为四个方程： image.png 方程的左边是接收器的 未知位置 到 红， 绿， 蓝， 黄 四个发射器用 3D 勾股定理计算出来的距离。 右边是从四个发射器到接收器的时间 t， 未知的接收器的偏差 b. 最终解这组方程从而得到接收器的位置 x y z 和时间偏差 b
  • 到这里我们目前建立的这套体系已经能够在距离地标较近的情况下，正确地计算我们的位置和时钟偏差.

像 GPS 那样对整个地球都可用

  • 传输介质: 不用可见光而是用 电磁辐射 的另一种形式 - 特定频率的电磁波
  • 信号发射源的可见性
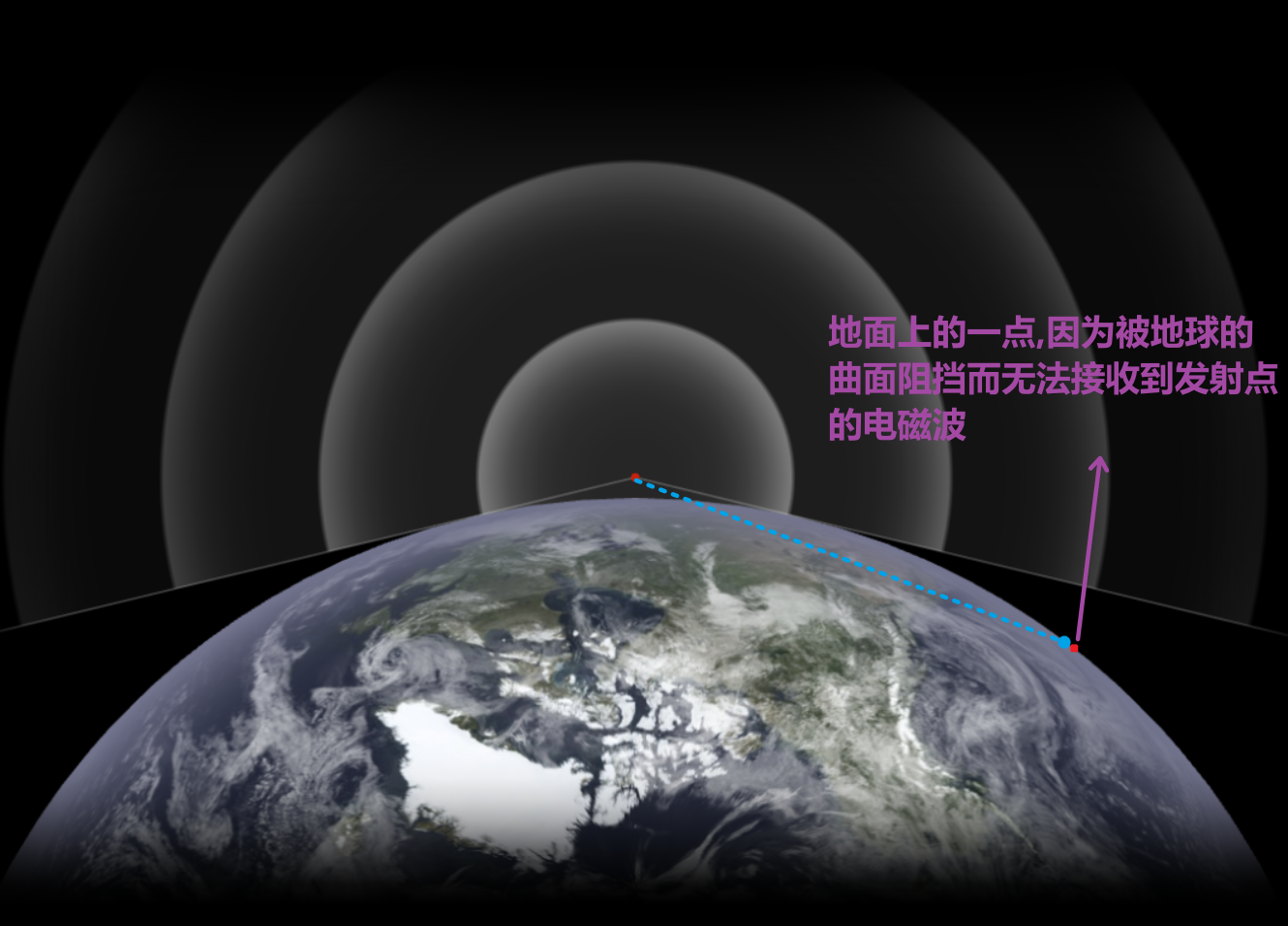
    • 我们所处的环境不是平坦的, 电磁波遇到山丘会被阻挡
      • 解决办法: 将发射器升到足够高
  • 地球本身有曲率, 是球状,而非平面
    • 地球曲率本身就像山一样遮挡了 发射器 的视平线: 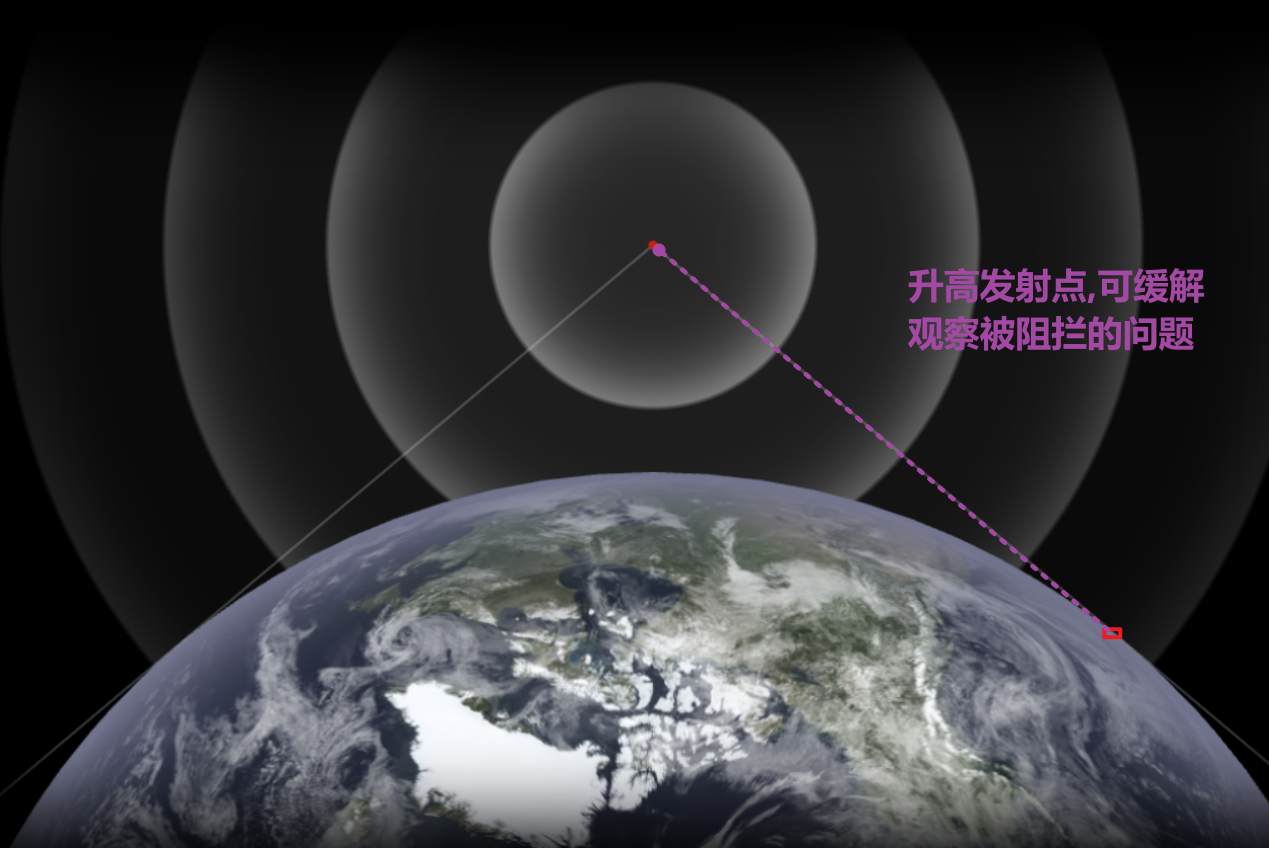image.pngimage.png 我们把 发射器 放得越高，能看到的区域就越大: image.png 因此,我们需要卫星携带发射器.